query on conservationlaws returned matrix

[yewalenikhil65]

Hi, @kaandocal
This is about conservationlaws
The way i understand this is, smith normal form was used to find the nullspace of netstoichmat(rn)

example taken from https://github.com/SciML/Catalyst.jl/blob/master/test/conslaws.jl

rn = @reaction_network begin
    (1, 2), A + B <--> C 
    (3, 2), D <--> E 
    (0.1, 0.2), E <--> F
    6, F --> G
    7, H --> G
    5, 0 --> K
    3, A + B --> Z + C
end

N = netstoichmat(rn)

julia> C = conservationlaws(N)
3×10 Matrix{BigInt}:
  0  0  0  1  1  1  1  1  0  0
 -1  1  0  0  0  0  0  0  0  0
  0  1  1  0  0  0  0  0  0  0

which returns vector of conserved quantities as

julia> C*states(rn)
3-element Vector{Any}:
 D(t) + E(t) + F(t) + G(t) + H(t)
 B(t) - A(t)
 B(t) + C(t)

I use a little different approach to check C matrix. Following is the nullspace estimate from rational basis perspective, meaning the way we would have done to calculate nullspace had we done it by hand. (Code logic taken from null.m in MATLAB and used RowEchelon.jl library to obtain rref)

using LinearAlgebra
using RowEchelon
function rational_basis_nullspace(A::AbstractVecOrMat)
"""
Citation:
This function is re-written in Julia , based on
Built-in MATLAB function null.m ( Copyright 1984-2017 The MathWorks, Inc.)
"""

    R,pivcol = rref_with_pivots(A)
    m,n = size(A);
    r = length(pivcol);
    nopiv = collect(1:n);
    deleteat!(nopiv, pivcol)
    Z = zeros(n,n-r);
    if n > r
        Z[nopiv,:] = diagm(0 => ones(n-r));
        if r > 0
            Z[pivcol,:] = -R[1:r,nopiv];
        end
    end
    return Z
end

This returns conservation laws as follows

julia> rational_basis_nullspace(N)'*states(rn)
3-element Vector{Any}:
 B(t) - A(t)
 A(t) + C(t)
 D(t) + E(t) + F(t) + G(t) + H(t)

As noticed, B(t) + C(t) conserved quantity earlier from conservationlaws is now A(t) +C(t)..
To notice further difference lets see the entries returned by LinearAlgebra.nullspace() and conservationlaws() as follows

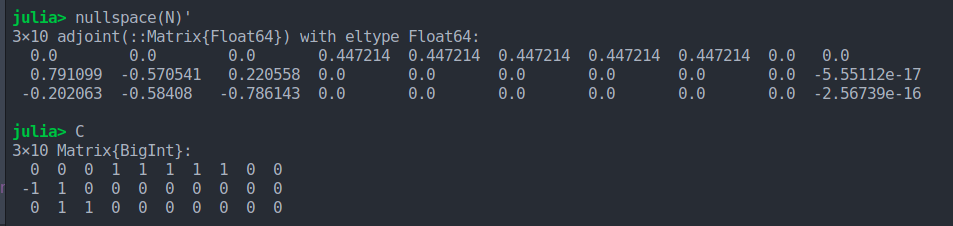
It seems some entries returned from conservationlaws don't agree with LinearAlgebra.nullspace and rational_basis_nullspace (even after appropriate scaling etc.) in a sense that expected conservedquantities differ by both approaches

[yewalenikhil65]

To further support my understanding, I have tried finding nullspace using QR factorization approach too..
Based on paper Conservation analysis of large biochemical networks
The conservationlaws/conserved quantities returned seem to match one i get from my rational_basis_nullspace function

using Catalyst
using LinearAlgebra
using RowEchelon
rn = @reaction_network begin
    (1, 2), A + B <--> C 
    (3, 2), D <--> E 
    (0.1, 0.2), E <--> F
    6, F --> G
    7, H --> G
    5, 0 --> K
    3, A + B --> Z + C
end
ns = numspecies(rn)
N = netstoichmat(rn)
Q,R = qr(N)  # QR decompsoition
Rᵣᵣₑ,pivots = rref_with_pivots(R)   # pivots ..useful for permuting the entries of independent species 
julia> Rᵣᵣₑ
10×10 Matrix{Float64}:
 1.0  1.0  -1.0  0.0  0.0  0.0  0.0   0.0  0.0  0.0
 0.0  0.0   0.0  1.0  0.0  0.0  0.0  -1.0  0.0  0.0
 0.0  0.0   0.0  0.0  1.0  0.0  0.0  -1.0  0.0  0.0
 0.0  0.0   0.0  0.0  0.0  1.0  0.0  -1.0  0.0  0.0
 0.0  0.0   0.0  0.0  0.0  0.0  1.0  -1.0  0.0  0.0
 0.0  0.0   0.0  0.0  0.0  0.0  0.0   0.0  1.0  0.0
 0.0  0.0   0.0  0.0  0.0  0.0  0.0   0.0  0.0  1.0
 0.0  0.0   0.0  0.0  0.0  0.0  0.0   0.0  0.0  0.0
 0.0  0.0   0.0  0.0  0.0  0.0  0.0   0.0  0.0  0.0
 0.0  0.0   0.0  0.0  0.0  0.0  0.0   0.0  0.0  0.0

julia> pivots    # index of independent species
7-element Vector{Int64}:
  1
  4
  5
  6
  7
  9
 10

# index of dependent species can be found by setdiff(1:ns, pivots)

julia> states(rn)[pivots]   # independent species...   
7-element Vector{Term{Real, Nothing}}:
 A(t)
 D(t)
 E(t)
 F(t)
 G(t)
 K(t)
 Z(t)


Rₙ = hcat(Rᵣᵣₑ[:,pivots],Rᵣᵣₑ[:,setdiff(1:size(Rᵣᵣₑ,2),pivots)])  # rearrange the pivots, to put independent species on one side and dependent on other
julia> Rₙ    # arranged as [Identity_matrix  !Identity matrix]
10×10 Matrix{Float64}:
 1.0  0.0  0.0  0.0  0.0  0.0  0.0  1.0  -1.0   0.0
 0.0  1.0  0.0  0.0  0.0  0.0  0.0  0.0   0.0  -1.0
 0.0  0.0  1.0  0.0  0.0  0.0  0.0  0.0   0.0  -1.0
 0.0  0.0  0.0  1.0  0.0  0.0  0.0  0.0   0.0  -1.0
 0.0  0.0  0.0  0.0  1.0  0.0  0.0  0.0   0.0  -1.0
 0.0  0.0  0.0  0.0  0.0  1.0  0.0  0.0   0.0   0.0
 0.0  0.0  0.0  0.0  0.0  0.0  1.0  0.0   0.0   0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0   0.0   0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0   0.0   0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0   0.0   0.0


m=length(pivots)   # number of independent species
new_states = vcat(states(rn)[pivots], states(rn)[setdiff(1:ns,pivots)])  # permuted states.. such that [independent_species; dependent_species]
l₀ = -Rₙ[1:m,m+1:end]'
julia> cons_law = [l₀ I]*new_states  # where [l₀ I] is conservationlaws matrix
3-element Vector{Any}:
 B(t) - A(t)
 A(t) + C(t)
 F(t) + G(t) + H(t) + 0.9999999999999999D(t) + 0.9999999999999999E(t)

Notice this matches with what i got using rational_basis_nullspace function

[yewalenikhil65]

Another shorter example to showcase the difference

rn = @reaction_network begin
    k1, ES --> E+S1
    k2, S1 --> S2
    k3, E + S2 --> ES
end k1 k2 k3

# from exsiting `conservationlaws()` function in Catalyst
julia> conservedquantities(states(rn),conservationlaws(netstoichmat(rn)))
2-element Vector{Any}:
 E(t) + ES(t)
 S1(t) + S2(t) - E(t)

# from rational_basis_nullspace function written in 1st comment in this issue
julia> rational_basis_nullspace(N)'*states(rn)
2-element Vector{Any}:
 E(t) + ES(t)
 ES(t) + S1(t) + S2(t)

# from QR factorization method , Based on paper Conservation analysis of large biochemical networks
ns = numspecies(rn)
N = netstoichmat(rn)
Q,R = qr(N)  # QR decompsoition
Rᵣᵣₑ,pivots = rref_with_pivots(R)

Rₙ = hcat(Rᵣᵣₑ[:,pivots],Rᵣᵣₑ[:,setdiff(1:size(Rᵣᵣₑ,2),pivots)])
m=length(pivots)   # number of independent species
new_states = vcat(states(rn)[pivots], states(rn)[setdiff(1:ns,pivots)])
l₀ = -Rₙ[1:m,m+1:end]'
julia> cons_law = [l₀ I]*new_states
2-element Vector{Any}:
 E(t) + 0.9999999999999999ES(t)
 S1(t) + S2(t) + 0.9999999999999998ES(t)

exsiting conservationlaws() / conservedquantities()function in Catalyst clearly yield different result from rational_basis_nullspace and QR method.(later two method giving similar conserved quantities)

[kaandocal]

Hey,

To clarify: the conservation laws are not unique since any linear combination of conserved quantities is itself conserved. Currently the code finds a basis (over the integers) for the set of all conserved quantities, which is the left null space of the matrix, and this basis is not unique in general.

As noticed, B(t) + C(t) conserved quantity earlier from conservationlaws is now A(t) + C(t)

Since B(t) - A(t) is a conserved quantity in both cases, note that B(t) + C(t) - (B(t) - A(t)) = A(t) + C(t), so we can recover one from the other by adding/subtracting B(t) - A(t).

Using Float64 arithmetic as done by LinearAlgebra.nullspace is not the best way to go at it; for your example in the first post the rightmost column should be 0 but is not due to numerical precision. The first rows agree up to rescaling, and the second and third rows both span the same space for the two matrices, meaning that the conserved quantities are all linear combinations of each other. SNF has the advantage of being exact and returning integral conservation laws, which is useful in many cases.

So in summary a) conserved quantities are not uniquely defined (only up to linear combinations) and b) we prefer integer coefficients. Does this clarify things a bit? :)

[yewalenikhil65]

Hey,

To clarify: the conservation laws are not unique since any linear combination of conserved quantities is itself conserved. Currently the code finds a basis (over the integers) for the set of all conserved quantities, which is the left null space of the matrix, and this basis is not unique in general.

As noticed, B(t) + C(t) conserved quantity earlier from conservationlaws is now A(t) + C(t)

Since B(t) - A(t) is a conserved quantity in both cases, note that B(t) + C(t) - (B(t) - A(t)) = A(t) + C(t), so we can recover one from the other by adding/subtracting B(t) - A(t).

Using Float64 arithmetic as done by LinearAlgebra.nullspace is not the best way to go at it; for your example in the first post the rightmost column should be 0 but is not due to numerical precision. The first rows agree up to rescaling, and the second and third rows both span the same space for the two matrices, meaning that the conserved quantities are all linear combinations of each other. SNF has the advantage of being exact and returning integral conservation laws, which is useful in many cases.

So in summary a) conserved quantities are not uniquely defined (only up to linear combinations) and b) we prefer integer coefficients. Does this clarify things a bit? :)

thanks @kaandocal for going thorugh this issue. I forgot that nullspace returns combinations that may not be unique.Your answer cleared my doubt.
Do you think matrix decomposition methods like QR or LU be more efficient than SNF for left nullspace calculations ? I read your comment somewhere that SNF could be O(n^3)

[kaandocal]

We need exact determination of the nullspace using integer arithmetic. Most standard algorithms like the LU or QR decomposition do not work over the integers (and SNF is basically the SVD over the integers). We briefly discussed the need for better/faster algorithms at #337 but I'm currently not aware of any...

[yewalenikhil65]

We need exact determination of the nullspace using integer arithmetic. Most standard algorithms like the LU or QR decomposition do not work over the integers (and SNF is basically the SVD over the integers). We briefly discussed the need for better/faster algorithms at #337 but I'm currently not aware of any...

Thanks for the discussion on this !
Will mention here if i come across any such method for larger systems. Closing this issue for now