62 不同路径

[royIdoodle]

62. Unique Paths 不同路径

难度: Medium

刷题内容

原题连接

• https://leetcode-cn.com/problems/unique-paths/

内容描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

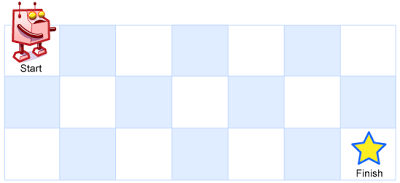
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

解题方案

思路 1 排列组合方式

例子中，m=7、n=3，也就是说，可以向右走6步（m-1）和向下走2步（n-2）；
如果用符号→表示向右走，符号↓表示向下走，那么这道题就变成了，(m-1)个→和(n-1)个↓有多少种排列组合方式，也就是最终

计算公式：(m-1 + n-1)! ÷ （(m-1)! × （n-1）!）

自行实现阶乘计算函数——factorial即可

代码：

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
// 为了提高算法效率，利用cache缓存计算结果
let cache = {
  1: 1
}
var uniquePaths = function(m, n) {
  return factorial(m + n - 2) / factorial(m - 1) / factorial(n - 1)
};

function factorial(num){
  if(num <= 1) {
    return 1;
  } else if (cache[num]) {
    return cache[num]
  }else{
    let value = num * factorial(num-1);
    cache[num] = value;
    return value
  }
}

思路 2 模拟矩阵
- 时间复杂度: O(N)

- 空间复杂度: O(N)

如果用每个格子上的值表示，当前格子到左上角格子的走法数量的话，那么右下角格子的值就是最终结果，样子如下

1	1	1
1	2	3
1	3	6
1	4	10
1	5	15
1	6	21
1	7	28

发现规律，每个格子的值等于左侧格子值 + 上方格子值，所以用双层循环绘制表格，再去最后的值即可。

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function(m, n) {
  let metrics = [];
  for (let x = 0; x < m; x++) {
    for (let y = 0; y < n; y++) {
      if (!metrics[x]) {
        metrics[x] = []
      }
      if (y === 0 || x === 0) {
        metrics[x][y] = 1
      } else {
        metrics[x][y] = metrics[x][y - 1] + metrics[x - 1][y]
      }
    }
  }
  return metrics[m-1][n-1];
};