fun-algorithms-cpp

This is personal projects for "playing" algorithms with cpp. Let's have fun!

Part 1. Sorting Algorithms

Part 2. Trees

• Haffman Tree

Huffman Tree

导读

１.　为什么哈弗曼编码能降低传输成本？

２.　从哈弗曼树到哈弗曼编码

３.　实现哈弗曼树用到的数据结构：最小优先队列（即最小堆）

４．代码实现（C++）

１.　为什么哈弗曼编码能降低传输成本？

　　哈弗曼编码是一种数据无损压缩的方式。根据通信原理，我们想进行数字传输的信息，如图像、声音文字等都是编码成“010101...”的二进制信号后再进行传输和解码。如果我们对这些需要编码的信息，比如英文里的26个字母，进行无差别编码，即每个字母都用相同比特位的二进制来编码时，其实是很不公平的。背过单词的我们知道，有些字母的出现频率很高，比如字母a，而有些字母出现频率很低，比如z，如果不加区分来进行编码，其实是很浪费的。

　　既然这样，何不用更小的二进制位数来编码大概率的字母，而用更大的二进制位数来编码小概率的字母，从而使总体编码长度的期望降低呢？

　　举个栗子，比如对下面一段字符串：

ＡＢＣＤＤＤＥＥＥＦＦＦＦＦＦＧＧＧＧＧＧ

一共有Ａ-G七个字符，其中A,B,C均出现一次，D,E均出现3次，F和G都出现了6次。如果无差别编码，我们可以用 $[log_27]+1=3$ 位二进制进行编码。既然无差别，我们不妨认为从A-G的编码依次为000,001,010,011,100,101,110。那么一共的编码的长度为: $$ 3\times(13+32+6*2)=63 $$ 　　可是如果根据出现频率不同，我们将它们的编码改为：

A: 00000
B: 00001
C: 0001
D: 001
E: 01
F: 10
G: 11

　　那么，所需的编码长度降为:
$$ 51+51+41+33+23+26+2*6 = 53 $$ 　　可见当高频字母的编码长度减小，而对应的低频字母的编码长度增大，最终的总长度减小，传输成本降低。而另一个关键点在于，由于上述编码为不等长编码，我们在解码的时候怎么样判断是哪个编码呢？仔细观察就可以发现，上述编码悄咪咪地满足一个条件：**每个完整编码都不是任何另一个编码的首码，这就保证解码结果准确且唯一。**其实这个编码就是用哈弗曼编码（Huffman code）实现的，下面详述一下实现过程。

２.　从哈弗曼树到哈弗曼编码

　　实现哈弗曼编码用到的数据结构是哈弗曼树。哈弗曼树具有以下几个特点：

1. 二叉树
2. 带权路径长度最小二叉树

　　

带权路径最小是什么意思呢？

N个给定权值作为叶子结点，其每个叶子结点带权路径长度为其权值乘以其到根节点的路径长度（也可以看作是该叶子结点的高度），记为 $W_i$ ；所有N个带叶子结点的带权路径长度即为该二叉树的总带权路径长度，记为WPL。

$$ WPL = \sum_{i=1}^N W_i $$

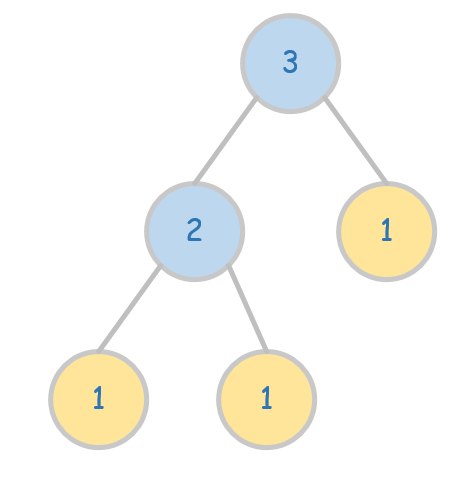
　　比如下面这棵树，

图1. 带权值的二叉树。 $$ WPL = W_1+W_2+W_3 = 12+12+1*1=5 $$

那么如何构建哈弗曼树呢（实现哈弗曼树的方法不唯一，这里只介绍其中一种）。

　　我们将上一part的例子继续拿过来，其中讲到的字符串中各个字母出现的频率如下：

A: 1
B: 1
C: 1
D: 3
E: 3
F: 6
G: 6

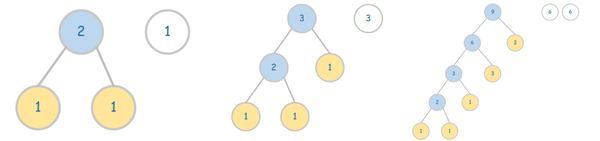
　　将其中七个频率值作为七个带权重的叶子节点，如下图所示：

图2. 七个带权重的叶子结点。

　　然后通过下面步骤构建哈弗曼树 （如图3所示，其中叶子结点用黄色标记）：

1. 将这七个节点看作七棵二叉树，那么它们都是只有根节点的二叉树，这七棵树组成一片森林。
2. 每次从森林中挑选根节点最小的两棵树，新建一个根节点，其值为选中的两棵树的根节点值之和，并将这两棵树分别作为新建根节点的左子树和右子树。
3. 重复步骤2，直到森林中只剩一棵二叉树。

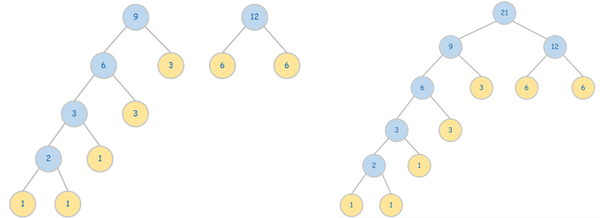
图3. 哈弗曼树构建过程。

　　我们可以来计算一下构建好的哈弗曼树的WPL值: $$ WPL = \sum_{i=1}^7 W_i\ = 15 + 15+14+33+32+62+6*2=53
$$ 　　从上图也可以看出，哈夫曼树的构建方法是自底向上的。且由于每次挑选的是权值最小的根节点，保证了权值越大的节点高度越小，而权值越小的节点高度越大，从而使得总体花费最小。　　

　　那么，如何从哈弗曼树到哈弗曼编码呢？二叉树，二进制，0和1，好像冥冥中有种联系？

没错的，每个叶子结点是我们需要编码的字母的频率值，我们可以根据从根节点到各个叶子结点的路径确定其编码值，即：

从根节点出发，每次往左边走，我们记为0；每次往右边走，我们记为1。

比如最左的叶子结点，走了五步，每次都是往左，因此其编码为00000。其实之前稍微剧透了一下，上一节中说到的根据出现频率的编码就是用这课实现的哈弗曼树实现的。

３.　实现哈弗曼树的数据结构：最小优先队列（即最小堆）

　　从上一节可知，在构建哈弗曼树的过程中，我们每次每次都会选出值最小的两个根节点，所以很自然地想到能够在 $O(1)$ 直接取出最小值，并用 $O(lgN)$ 维护其结构的：

最小堆 （minimum heap）

它还有个更为炫酷的名字：最小优先队列。

　　第一次接触“堆”这种数据结构是在学习“堆排序”的时候，如果说快速排序给我的是一种智力上的简洁与惊艳感，堆排序则是从开始的“有必要这么复杂吗”到“太惊艳了”。快速排序就像天山折梅手，精简而强大；堆排序就像小无相功，不着形迹却威力无穷。

　　扯远了，这篇文章只介绍一下这种数据结构为什么适用于实现哈弗曼编码。最小堆，是完全二叉树，且每个节点的值，均小于其左右孩子（如果有）的节点值。

　　因为是完全二叉树，因此堆可以直接用线性表存储（详见上一篇博客）。另一方面，其根节点的值即是所有节点的最小值，即找最小值的时间为 $O(1)$ 。而取出最小值后，需要维护堆的结构使其满足最小堆的性质，具体如下：

１. 将根节点与最后一个叶子节点对调，取出最后的节点，即得到最小值；

2. 将此时新的根节点和其左右孩子比较：
3. 如果比他们都小，那么依旧满足最小堆性质；
4. 如果不是最小，和最小的对调，并在对应的子树中逐层检查并维护最小堆的性质。

　　可以看出，维护最小堆需要的的时间为 $O(h) $（h为二叉树的高度），而根据完全二叉树的性质可知， $h=\left[ log_2N \right]+1$ （N为节点个数）。

　　在C++中有现成的实现最小优先队列，也即最小堆的容器：

priority_queue<int, vector<int>,greater<int>> q;

　　回到哈弗曼树，每次我们取出两个最小的根节点，并求出他们的和：

int sum = q.top()
q.pop();
sum+=q.top()
q.pop()

　　然后将新的根节点的值，也即求得的和值插入最小优先队列：

q.push(sum)

　　如此直到队列为空，即可自底向上地得到哈弗曼树的节点值。

４．代码实现（C++）

这一段并不打算直接贴代码。。。

　　其实这篇学习笔记是听一门数据结构课的OJ作业，题目也不是实现哈弗曼编码，而是根据已有的字母和频率值，判断几个实现的编码是否哈弗曼编码，因为实现哈弗曼编码的方法不唯一，因此并不实现哈弗曼编码，而是根据下面两个条件判断是否符合：

1. 根据哈弗曼树的构建过程，通过上述最小优先队列的实现方法，得出最小的WPL值，也即最小的cost；然后计算每种编码方法的cost，如果大于预期最小的cost，那么就不是哈弗曼编码。
2. 如果不大于最小的cost，那么要请出另一个条件，也即之前反复强调的：为了能准确且唯一地解码，判断是否某段编码是其它编码的首码。如果是，那么就不是哈弗曼编码。

© 2019 GitHub, Inc.