-
Notifications
You must be signed in to change notification settings - Fork 248
Jacobi Theta functions #394
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Conversation
Implementations, tests, and ULP plotting programs are provided for the four Jacobi Theta functions per #373. Twenty-four public C++ functions are provided in all, covering various precision-preserving scenarios. Documentation for collaborators is provided in the code comments. Proper documentation for end users will be provided when the implementation and APIs are finalized. Some tests are failing; this implementation is meant to start a conversation. The core dilemma faced by the author was that large values of |q| resulted in slow convergence, and sometimes wildly inaccurate results. Following the implementation note in DLMF 20.14, I added code to switch over to the imaginary versions of the theta functions when |q| > 0.85. This restored accuracy such that all of the identity tests passed for a loose-enough epsilon, but then lost precision to the point that the Wolfram Alpha spot checks failed. It is the author's hope that someone with floating-point experience can tame the exponential dragons and squeeze the ULPs back down to a reasonable range when |q| is large. When #392 is merged I will add more thorough value tests, although I fully expect them to fail until the underlying precision issues are resolved. As a final note, the precision issues do not affect the z=0 case - the ULP plots indicate these return values within 2 ULP across all valid |q|. So that's a start.
|
That looks really good! You can save me some time by providing a couple of concrete examples which currently have low accuracy? |
|
@jzmaddock I can provide specific examples later today but the failing spot tests ( To be clear: the real-valued code paths are inaccurate for large q. The Just so you know: the Will provide actual examples tonight if I haven't heard from you. |
|
OK I have a test case, thanks. Minor nits while I think of them:
After that the error rates don't look bad (200eps or so), but.... as an example jacobi_theta_2(3, 0.9921875) is so totally trivial to calculate (done in one iteration, and I don't see any obvious things that would loose precision) that I would like to investigate some more. One possible improvement is in: where log(q) might be better expressed as log1p(q-1) when q is ultra close to 1, but makes no difference in the case above. And I'm not completely convinced it ever would make a difference, I need to think about that ;) |
|
One more nit: if you instantiate with for example The error in the case above come entirely from the line The issue being that z(2n-z/pi) happens to evaluate to very close to pi in this case. I don't see any algebraic simplification though? |
Thanks
Will do
Aha! I never would have thought of that. It likely affects the use of I'll make these changes and report back. |
|
@evanmiller : It'll probably a few iterations on this, so make sure to tag your commits with Also, could you drop a performance benchmark into |
* Add tests covering z=0 special values from MathWorld * Add missing real_concept header * Replace M_PI and friends with constants::pi etc * Use BOOST_MATH_STD_USING in more places
|
I've made the changes suggested and added a few more tests covering special values (did you know the third theta function is related to the gamma function?). I don't see any perceptible change to the test results though. @NAThompson I will look into adding a performance benchmark later tonight. |
|
Good news! I think I've just about cracked the precision issues. I completed the square on the exponentials, and rewrote them as double-sided summations following DLMF 20.13.4 and 20.13.5. The mean errors on the MathWorld data are now down to <10 (eps? ULPs? whatever BTW What are we benchmarking against exactly? I don't see Jacobi theta functions in either GSL or RMath. Commit incoming. |
Ourselves! Run the benchmark under |
Rewrite the private imaginary versions to use double-sided summations following DLMF 20.13.4 and 20.13.5. This cuts down the worst of the precision issues by a factor of 10, and gets more of the tests to pass. I am confident enough in the code path to eliminate the compile-time __JACOBI_THETA_USE_IMAGINARY flag. In fact the imaginary-z code paths are now enabled for all |q| > 0.04, i.e. most legal values of q. More extensive tests will be needed to illuminate any remaining precision issues.
| jacobi_theta3tau(constants::quarter_pi<RealType>() - z, tau) * jacobi_theta3tau(constants::quarter_pi<RealType>() + z, tau), | ||
| eps); | ||
|
|
||
| _check_close( // DLMF 20.7.19 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
If you want, you can use my "math_unit_test.hpp" and use CHECK_ULP_CLOSE if you think it'll be a bit more ergonomic. It also compiles much faster that Boost.Test.
* Add LICENSE notice to main file * Document convergence criteria * Eliminate eps*eps = 0 logic. This causes some disagreement with the zero returned by Wolfram Alpha for z=0, q > 0.99 in the fourth function. Mathematically, the fourth function is never exactly zero, so I don't trust Wolfram here. * Per code-review comments, remove multiplications by floating-point 2. * Tweak the plotting programs to display their titles, and to uniformly use `float` as their CoarseType and `long double` as their `PreciseType`.
| // Internal convergence criterion: | ||
| // If the delta is more than an absolute epsilon, keep going. | ||
| // If the delta is more than an relative epsilon, and the denominator | ||
| // is non-zero, keep going. |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I'm not sure this comment is very informative; I was hoping for something like "expected error is cond(f; x)eps/2, so when delta <..." and then some perturbative analysis.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
The comment represents the extent of my thinking and, well, education. I'm happy to incorporate a more formal convergence analysis but it's simply outside my ken.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
lol, alright np. I'll see if I can get a minute to work out some error analysis for these functions.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
IMO there's no need to require delta < eps, normally we would just use abs(result * eps) > abs(delta) as if that's true, then adding delta can have no effect on result. The only exception would be if delta can grow as well as shrink.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
The sign of delta can alternate, which could theoretically put result at 0 after two iterations. So I wanted to handle that somehow, and distinguish the situation from an underflow.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Wait then aren't all these calls to abs superfluous?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Sorry, I should have said: the numerator is q_n (always positive) but the denominator is result (which may oscillate). It would probably be better to change the denominator to previous_q_n.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I personally might track \sum q^{n^2} since it provides a nice L1 bound on the sum.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I'm not sure the sum will work because of the alternating signs. In addition to the oscillating component there is the (-1)^n in two of the formulas. With q close to 1, the straight sum could be large relative to the final result, and so an error that is small relative to the sum may be large relative to the result.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I have updated the convergence criterion to compare q_n to the previous one. Everything including ULP plots look pretty much the same. Let me know what you think.
The quadrature tests revealed a problem in the m1 functions: they too should switch to the _IMAGINARY logic for q > exp(-pi), or will suffer from slow convergence. Fix them. Also tighten tolerances for many tests from sqrt(eps) to 100 * eps.
|
|
||
| The following [link math_toolkit.ulps_plots ULPs plot] is representative, fixing /q/=0.5 and varying /x/ from 0 to 2[pi]: | ||
|
|
||
| [graph jacobi_theta1_float] |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Looking at this graph, it appears that the x->0 accuracy is not limited by the condition number of function evaluation and hence it could be implemented better. Is this a case to recommend use of jacobi_theta1tau?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
tau can help with precision issues on q but not x.
|
|
||
| [equation jacobi_theta2] [/ \theta_2(x, q) = 2 \sum_{n=0}^\infty q^{(n+\frac{1}{2})^2} \cos((2n+1)x) ] | ||
|
|
||
| Or in terms of an imaginary [tau]: |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I'm confused. You say you enforce that tau is purely imaginary, yet your function signature says tau is the same type as x. . .
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
tau the C++ argument is real-typed. The provided number is implicitly multiplied by i. This seemed simpler than trying to provide a complex-valued API.
| #include <boost/math/tools/test_data.hpp> | ||
| #include <boost/test/included/prg_exec_monitor.hpp> | ||
| #include <boost/math/special_functions/jacobi_theta.hpp> | ||
| #include <fstream> |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I don't understand what this file is doing. It appears you are spitting out values of the function from your own code; but isn't that tautologous?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
This is what the other tools/*_data.cpp files do – use a high-precision implementation to compare against the low-precision implementations.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Sort of, here's how I approach this:
Let's say we have a principal method, plus a bunch of special case handling (asymptotic expansions at one end of the range say as an example). The main things that can go wrong:
- The principal method has an outright bug (eg terms in series not correctly calculated).
- The principal method looses precision due to either cancellation or an incorrect termination condition.
- There are bugs in the special cases, or the selection logic between them.
We can deal with (1) by comparison to a "known good" - so job done on that I think.
For (2) and (3) what I try and do is calculate spot values at very high precision using the principal method alone, the important thing is to remove all the special case handling as otherwise as @NAThompson says you're not really testing much. In an ideal world you would use a completely different method, but those are really hard to find. When I remember, what I should have done (but didn't always) is archive a "naive" version of the principal method in the test value generator file and call that rather than the actual method - I suspect I may have been sloppy and just quickly commented stuff out in the header occasionally though :(
However, with regard to different methods: do the defining series for these functions satisfy that? They don't have to be fast for test value generation as they're only run the once. In extreme cases (1F1) I've resorted to interval arithmetic using mpfi_float to handle series with lots of cancellation when generating spot tests.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
That makes sense. We have essentially two implementations of each function, the IMAGINARY path (for tau < 1) and the regular path. The code chooses the one that is expected to converge more quickly. So one possibility would be to invert the branch logic so that the test data always chooses the slower path when generating test data.
|
@evanmiller : Could you drop this file into // (C) Copyright Nick Thompson 2020.
// Use, modification and distribution are subject to the
// Boost Software License, Version 1.0. (See accompanying file
// LICENSE_1_0.txt or copy at http://www.boost.org/LICENSE_1_0.txt)
#include <random>
#include <benchmark/benchmark.h>
#include <boost/math/special_functions/jacobi_theta.hpp>
#include <boost/multiprecision/float128.hpp>
#include <boost/multiprecision/mpfr.hpp>
#include <boost/multiprecision/cpp_bin_float.hpp>
using boost::multiprecision::number;
using boost::multiprecision::mpfr_float_backend;
using boost::multiprecision::float128;
using boost::multiprecision::cpp_bin_float_50;
using boost::multiprecision::cpp_bin_float_100;
using boost::math::jacobi_theta1;
using boost::math::jacobi_theta1tau;
template<class Real>
void JacobiTheta1(benchmark::State& state)
{
std::random_device rd;
std::mt19937_64 mt(rd());
std::uniform_real_distribution<long double> unif(0,0.01);
Real x = static_cast<Real>(unif(mt));
Real q = static_cast<Real>(unif(mt));
for (auto _ : state)
{
benchmark::DoNotOptimize(jacobi_theta1(x, q));
x += std::numeric_limits<Real>::epsilon();
}
}
BENCHMARK_TEMPLATE(JacobiTheta1, float);
BENCHMARK_TEMPLATE(JacobiTheta1, double);
BENCHMARK_TEMPLATE(JacobiTheta1, long double);
BENCHMARK_TEMPLATE(JacobiTheta1, float128);
BENCHMARK_TEMPLATE(JacobiTheta1, number<mpfr_float_backend<100>>);
BENCHMARK_TEMPLATE(JacobiTheta1, number<mpfr_float_backend<200>>);
BENCHMARK_TEMPLATE(JacobiTheta1, number<mpfr_float_backend<300>>);
BENCHMARK_TEMPLATE(JacobiTheta1, number<mpfr_float_backend<400>>);
BENCHMARK_TEMPLATE(JacobiTheta1, number<mpfr_float_backend<1000>>);
BENCHMARK_TEMPLATE(JacobiTheta1, cpp_bin_float_50);
BENCHMARK_TEMPLATE(JacobiTheta1, cpp_bin_float_100);
template<class Real>
void JacobiTheta1Tau(benchmark::State& state)
{
std::random_device rd;
std::mt19937_64 mt(rd());
std::uniform_real_distribution<long double> unif(0,0.01);
Real x = static_cast<Real>(unif(mt));
Real q = static_cast<Real>(unif(mt));
for (auto _ : state)
{
benchmark::DoNotOptimize(jacobi_theta1tau(x, q));
x += std::numeric_limits<Real>::epsilon();
}
}
BENCHMARK_TEMPLATE(JacobiTheta1Tau, float);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, double);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, long double);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, float128);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, number<mpfr_float_backend<100>>);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, number<mpfr_float_backend<200>>);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, number<mpfr_float_backend<300>>);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, number<mpfr_float_backend<400>>);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, number<mpfr_float_backend<1000>>);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, cpp_bin_float_50);
BENCHMARK_TEMPLATE(JacobiTheta1Tau, cpp_bin_float_100);
BENCHMARK_MAIN();Also, running this file, I find that something has gone wrong with the ADL for |
doc/sf/jacobi_theta.qbk
Outdated
| recommended, as the existing Boost implementations are likely faster and | ||
| more accurate. | ||
|
|
||
| Most applications will want to use the /q/ parameterization of the functions: `__jacobi_theta1`, `__jacobi_theta2`, `__jacobi_theta3`, and `__jacobi_theta4`, where /q/ is restricted to the domain (0, 1). However, a second [tau] parameterization is provided for all four functions, where |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Is there equivalent Mathematica syntax that has the same nome/tau/scaling conventions? It might be nice to put that in here . . .
I see EllipticTheta[a,q,z]
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I don't think Mathematica provides a tau parameterization. I'll add a link in the docs to EllipticTheta, though.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I'm getting more confused about the tau parametrization. It now looks to me like you are trading a multiplication on each iteration for a logarithm and a call to std::exp on each iteration. . .
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Implementing purely in q, without a log, would require a pow in place of the exp. The private IMAGINARY code paths have to do the exp anyway since they are implementing hyperbolic sine and cosine.
Exposing tau has the added benefit of letting the user provide a pre-logged argument for the sake of precision, e.g. with q close to 1 (so the user can use log1p) or if the argument provided would have been an exponential such as exp(-a).
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
You don't need a call to pow, since q^(n+1)^2 = q^n^2qnqn*q. Here's some pseudocode:
template<typename Real>
Real new_theta1(Real x, Real q)
{
using std::sqrt;
using std::sin;
using std::abs;
Real scale = 2*sqrt(sqrt(q));
Real term = sin(x);
Real sum = term;
size_t n = 1;
Real qn = q;
Real qnsq = q;
Real prefactor = qnsq*qn;
while (prefactor > abs(sum)*std::numeric_limits<Real>::epsilon())
{
term = prefactor*sin((2*n+1)*x);
if (n & 1) {
sum -= term;
} else {
sum += term;
}
qn *= q;
qnsq = qnsq*q*qn*qn;
prefactor = qnsq*qn;
++n;
}
return scale*sum;
}This executes in 13ns on my machine. More improvements are available from a Clenshaw recurrence.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Very cool! Happy to explore performance improvements after everything else is settled.
Will do! |
| RealType delta, partial_result = 0; | ||
|
|
||
| do { | ||
| delta = exp(-tau*z_n*z_n/constants::pi<RealType>()); |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Maybe precompute tau/constants::pi<RealType>() so that there isn't a division on each iteration.
People don't realize that elementary special function evaluations are in the same complexity class as division!
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
If we're going to squeeze out divisions like that, it might make sense to divide tau by pi further up the call stack.
|
|
||
| do { | ||
| q_n = exp(-tau * constants::pi<RealType>() * RealType(n + 0.5)*RealType(n + 0.5) ); | ||
| delta = q_n * sin(RealType(2*n+1)*z); |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Calling sin on each iteration seems expensive; can't it be done via a Clenshaw recurrence?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
The iteration count is typically between 2 and 5 so I'm not sure a recurrence formula will buy much (also because there's already an exp in each iteration).
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Ok, so most Clenshaw recurrence discussions descend rather than ascend, so we instead can use
sin((2(n+1)+1)x) = sin((2n+1)x)*cos(2x) + cos((2n+1)x)*sin(2x)
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Combine this with the recurrence for q^n^2 and you can do the whole thing with a single call to std::cos and std::sin and then only muls and adds after that.
|
|
||
| do { | ||
| q_n = exp(-tau * constants::pi<RealType>() * RealType(n + 0.5)*RealType(n + 0.5)); | ||
| delta = q_n * cos(RealType(2*n+1)*z); |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Clenshaw recurrence instead of cos on each iteration?
| // = 2 * Σ (-1)^n * exp(iπτ*(n+1/2)^2) * sin((2n+1)z) | ||
| template <class RealType, class Policy> | ||
| inline RealType | ||
| jacobi_theta1tau(RealType z, RealType tau, const Policy& pol) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Point of pedantry: I'd prefer it if the actual entry points followed the logic in https://www.boost.org/doc/libs/1_73_0/libs/math/doc/html/math_toolkit/special_tut/special_tut_impl.html, what we gain is the ability to handle arguments of different types (including integers), plus expression templates when used with multiprecision types.
On a related note, I'd like to see the entry points added to this test: https://github.com/boostorg/math/blob/develop/test/compile_test/instantiate.hpp,
Also note that each special function appears in multiple sections in that file - you will very likely get test failures when doing this, but it does catch a lot of issues - including now, not forwarding policies correctly ;)
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
To be clear - should I be using promote_args and friends in the public API? (I was advised against this previously.)
I've added the entry points (privately) to instantiate.hpp - lots of failures - will keep me busy tomorrow.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
How's it look now?
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
To be clear - should I be using promote_args and friends in the public API? (I was advised against this previously.)
Yeah, my bad, you had a complex number interface before and promote_args doesn't work (easily) with that. Now that it's all real-valued, might as well be consistent with everything else.
aside 1: promote_args is mis-named, should really be "make_common_floating_point_type" or something.
aside 2: I guess it would help if I updated it to function with complex number types as well!
I've added the entry points (privately) to instantiate.hpp - lots of failures - will keep me busy tomorrow.
Likely most will disappear once the argument type handling is in place.
How's it look now?
You're way ahead of me, will catch up with this later!
Add Jacobi theta functions to the instantiation tests and fix up everything needed to make them pass. This changes the function signatures to use promote_args.
This script broke when the promote_args API was added.
Compare the non-oscillating part of the delta to the previous one. This avoids some headaches comparing the delta to the partial sum, because the partial sum can be a small number due to the oscillating component alternating signs. Because successive terms involve either q^n^2 or exp(-(pi*n)^2), convergence should still happen pretty quickly. Graphs have been updated and tests still passs with no noticeable difference.
|
This looks like it's ready to go? @NAThompson ? |
|
I'm happy with this; the only potential point of improvement is using the trigonometric recurrence and the q^{n^2} recurrence to increase the speed. But perfect is the enemy of the good. |
|
@NAThompson's ideas may also yield accuracy improvements – but those can always take the form of a future PR. So you have my blessing to merge as well. |
|
Are the build errors on https://travis-ci.org/github/boostorg/math/builds/718417184 related to this PR? |
|
My bad; I told @evanmiller to |
|
Testing the "obvious" fixes now.... |
|
Tentative fixes pushed: just looks like the usual concept-failures. Glad someone was paying attention to develop results as I missed that! |
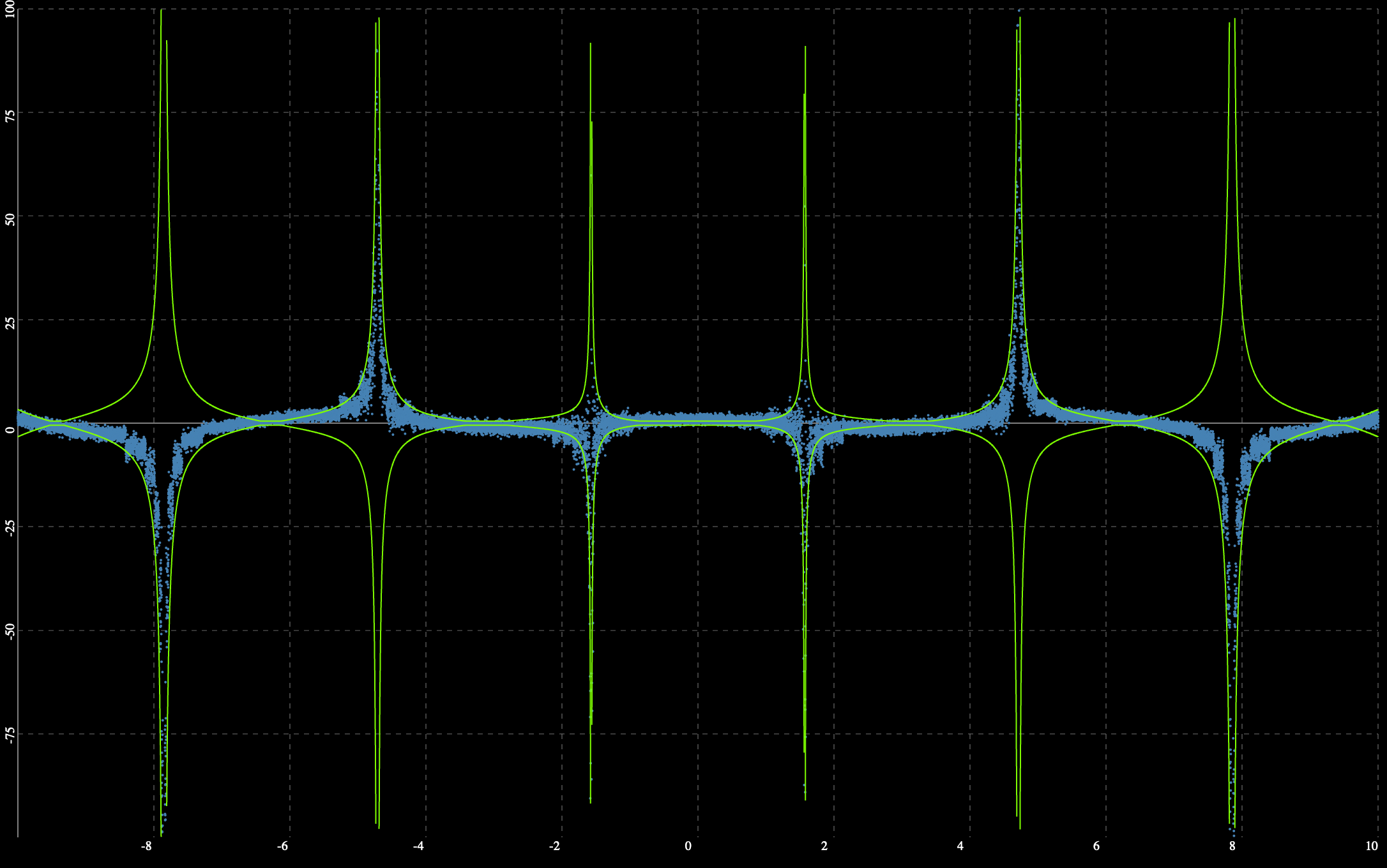
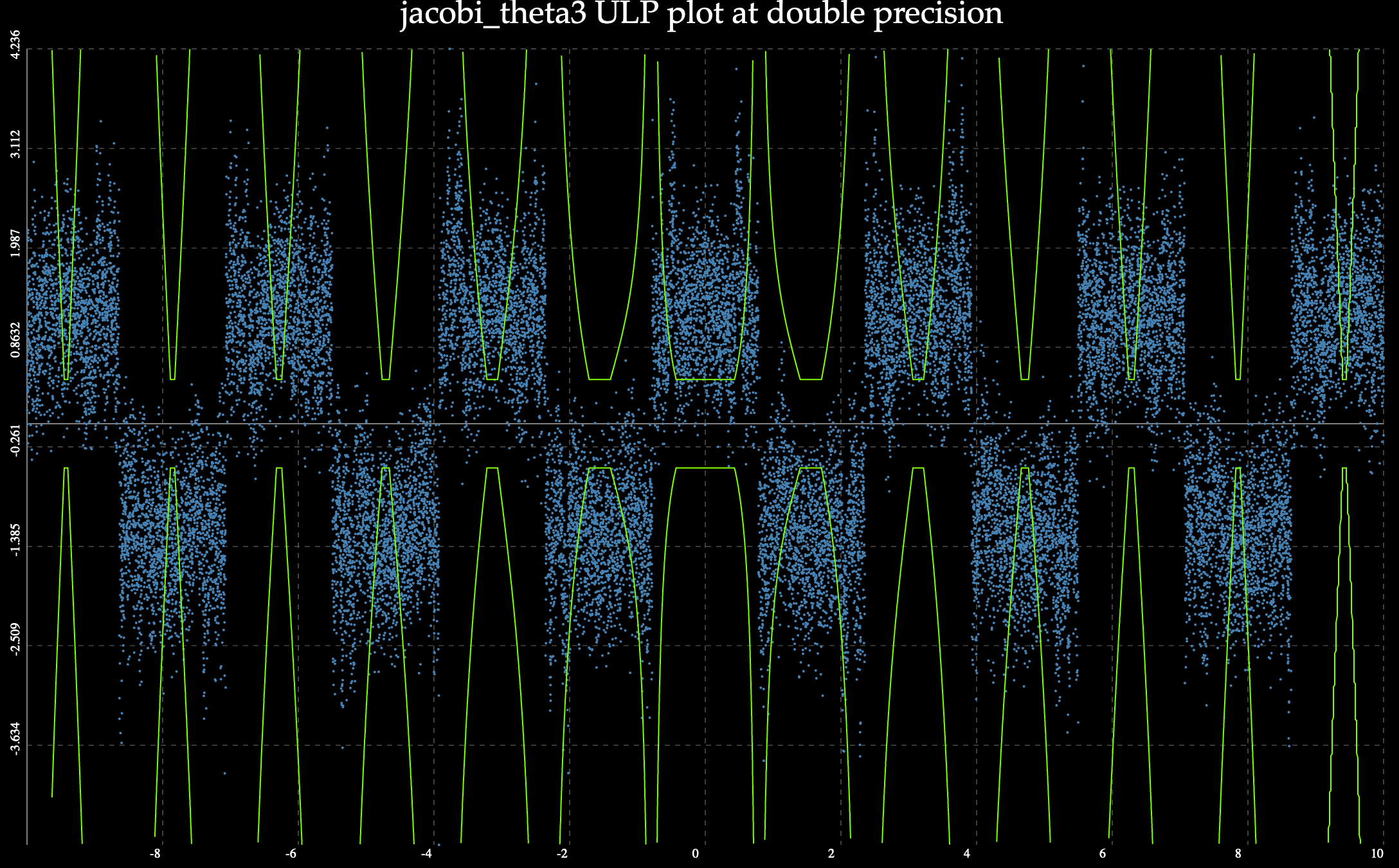
Implementations, tests, and ULP plotting programs are provided for the four Jacobi Theta functions per #373. Twenty-four public C++ functions are provided in all, covering various precision-preserving scenarios.
Documentation for collaborators is provided in the code comments. Proper documentation for end users will be provided when the implementation and APIs are finalized.
Some tests are failing; this implementation is meant to start a conversation. The core dilemma faced by the author was that large values of |q| resulted in slow convergence, and sometimes wildly inaccurate results. Following the implementation note in DLMF 20.14, I added code to switch over to the imaginary versions of the theta functions when |q| > 0.85. This restored accuracy such that all of the identity tests passed for a loose-enough epsilon, but then lost precision to the point that the Wolfram Alpha spot checks failed. It is the author's hope that someone with floating-point experience can tame the exponential dragons and squeeze the ULPs back down to a reasonable range when |q| is large.
When #392 is merged I will add more thorough value tests, although I fully expect them to fail until the underlying precision issues are resolved.
As a final note, the precision issues do not affect the
z=0case - the ULP plots indicate these return values within 2 ULP across all valid |q|. So that's a start.Any feedback appreciated.